Introduction to e-voting schemes

Given the availability of technology in our society as well as the need for tools supporting democratic decision making, it is not surprising that e-voting is a growing research field. But unlike suggested by their name, e-voting schemes are not only digitalized versions of traditional voting systems where paper ballots are counted by hand. They go a step further by leveraging cryptographic methods to provide privacy and verifiability guarantees. In particular, trust is shifted from the system to independent verifiers who can check that everything went well.
The aim of this post is to gain an understanding of how this type of systems works with a concrete example. We will go over some background information on voting schemes, give a description of the Helios 2.0 scheme, look into a possible attack and finish with a few pointers about key parts of a simplified implementation.
Types of voting schemes
In traditional voting systems, each voter puts a piece of paper carrying her vote in a box. Some trusted administrator then opens the box, counts the votes and publishes the result.
The class of schemes we are talking about follow the same pattern, except that instead of casting a piece of paper in a box, the vote is encrypted before being shared on a public bulletin board, i.e. a medium where anyone can read from. This allows observers to check some properties of the ballots without seeing their content since they are encrypted. The ballots can then be tallied by the organizer in possession of the necessary decryption material.
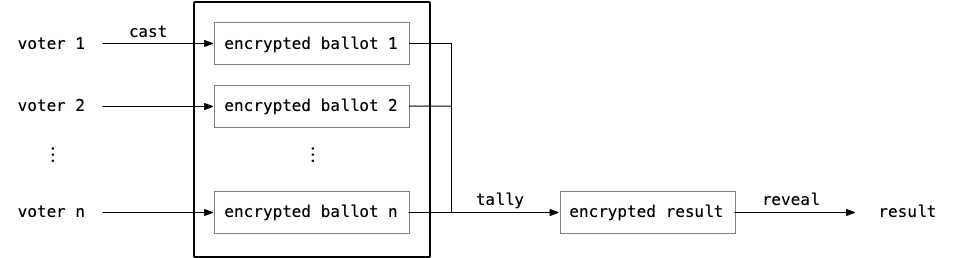
Voting schemes of this type aim at shifting the trust of the voters away from the system to some data published during the process. This means that instead relying on the system as a black-box, voters can be convinced of the integrity of the result by examining the public bulleting board. In parallel of being verifiable, these voting schemes naturally try to keep the content of each ballot hidden to preserve the privacy of the voters. We will see how this can be achieved in the next section.
In order to limit the scope of this post, we do not worry about the eligibility of the voters. In other words, we assume that another system checks whether a vote comes from a legitimate voter or not. But this does not prevent legitimate voters from colluding and potentially learning private information, as we will see later. Another assumption we make is the existence of an honest bulletin board, which is some sort of public database trusted to display everything that has been written on it. Lastly, we want to focus on verifiability and simplify the system presented in the following section by considering a single organizer; in the original scheme multiple organizers perform decentralized decryption to avoid a single point of trust, and for example to prevent an organizer from revealing the content of a ballot.
Helios
In this section we discuss the Helios 2.0 voting scheme initially described in [Adida2009]. It did not introduce novel techniques or constructions but Helios was the first e-voting system publicly accessible and it was used for official elections, thus a significant amount of literature exists on the topic. We begin by examining the verifiability property and how it motivates the design of this system.
What can be verified?
Let us start by being more precise on what we mean by verifiability. The main objective of this property is for an external verifier (not in possession of any secret key) to be able to distinguish whether the result of the vote is indeed the sum of the individual ballots cast by the voters. This is achieved in Helios by displaying the ballots and the result on a public bulletin board; using a special type of encryption, both of these data structures stay hidden while a verifier can still sum the ballots and check that the result is correct.
As a consequence of this encryption, the operation of creating an encrypted ballot as well as the action of revealing the result need to be verified. To this end, a proof certifying the validity of the encryption is added to the ballot by the voter, and similarly the organizer publishes a proof along the voting result ensuring that it corresponds to the summed ballots. But these two proofs are also public, thus they have to attest the validity of the encryption and decryption steps without leaking information about the choice of the voter or the secret key of the organizer. Cryptographic constructions called zero-knowledge proofs serve this purpose and we will describe later how they work and fulfill their role.
To reformulate, verifiability in Helios consists of three steps across the voting process certifying its integrity to an external verifier. First a zero-knowledge proof in each ballot attests that they are well formed, the special type of encryption then allows recalculation of the encrypted result, and finally a second zero-knowledge proof attests that the result is properly decrypted.
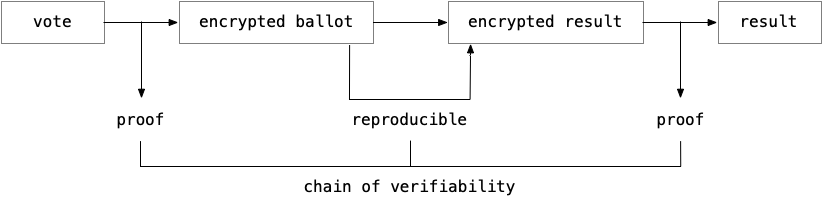
We will now describe how the voting scheme is used and built before coming back to the necessary building blocks, namely the encryption scheme and the zero-knowledge proofs.
Overview of the scheme
In this part we describe the participants of the voting process and which algorithms they execute.
Participants
As mentioned earlier, three kinds of participants have a role in this voting process. First comes the organizer, who takes care of generating the necessary encryption/decryption keys at the beginning and reveals the voting result at the end. The organizer has to be trusted to not share his part of the key. Second are the voters who, as their name suggests it, vote and cast an encrypted ballot. Lastly come the verifiers, who check the steps of the verifiability chain to make sure of the integrity of the process. Anyone, voter or external, can act as a verifier.
| Participant | Data | Role |
|---|---|---|
organizer |
secret key |
generate keys, tally ballots and provide a proof that the result is the decryption of the combined ballots |
voter |
public key |
build a ballot and publish it with a proof of its validity |
verifier |
public key |
verify that:
|
Algorithms
The Helios voting scheme is composed of five algorithms run by the organizer and the voters.
setup-
In this step the organizer generates the necessary cryptographic material. An asymmetric encryption scheme is used, thus a public and and a private (or secret) key are generated. The public key is shared to allow the voters to encrypt their vote with it, and the secret key is kept to decrypt the result at the end of the process. Note that in the original scheme, there is actually a group of organizers using distributed key generation to avoid a single point of trust and it is enough for a part of them to be honest to maintain the security guarantees.
vote-
Each voter uses this function to construct a ballot from her vote. This implies the encryption of the vote using the public key as well as the generation of some zero-knowledge proofs attesting that the vote is valid.
cast-
After building the ballot, each voter sends it to the public bulletin board, where it is visible to everyone.
tally-
This step can be executed by anyone thanks to the type of encryption used. The ballots stay encrypted while they are combined to form the encrypted result. More details in the next part.
reveal-
In the final step, the organizer uses her secret key to decrypt the encrypted result and reveals the voting result. A corresponding proof is also generated to attest that the result is indeed the decryption of the tally result.
During and after the voting process, verifiers can check that each step was executed properly by observing the data on the bulletin board.
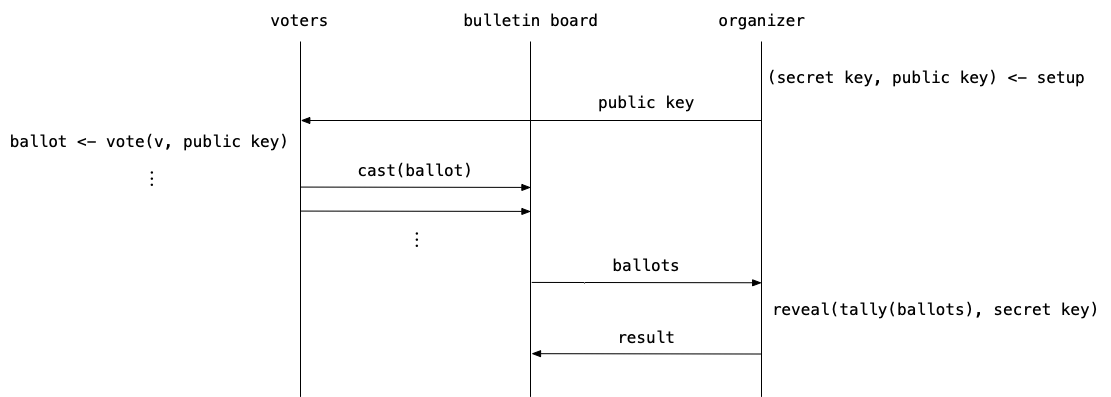
We will now discuss in more details how the encryption and the proofs of knowledge work in Helios.
Encryption
In general, encryption is a method to hide information and to be able to transmit it over an exposed channel.
Typically, a function called encrypt converts a plaintext message m into a ciphertext c which does not reveal anything about m.
Another function decrypt transforms c back into the recovered plaintext m', which should be identical to m.

In order to execute those functions, another piece of information called key is needed. In our context we are dealing with asymmetric encryption, which means that the key used to encrypt is different from the one for decryption. More concretely, a public key is needed to encrypt a vote into a ballot and the corresponding secret key allows the organizer to decrypt the voting result at the end. This means that the ballots on the bulletin board do not reveal anything about the underlying votes without access to the secret key.
Application in Helios
We consider the case where a vote is a sequence of 0’s and 1’s but at most one 1, indicating for which candidate the vote is. For example, (0, 1, 0) is a vote for the second candidate.
To form a ballot, each element of the vote is encrypted separately using a homomorphic encryption scheme.
This type of encryption allows the encrypted ballots to be combined element-wise with each other and the result contains the sum of the votes for each candidate.
The voting organizer holding the secret key can then reveal the result using her secret key.
- Homomorphic encryption
-
encrypt(a) * encrypt(b) == encrypt(a + b)
For example, let us consider a very small election where Alice and Bob choose among three candidates. Alice votes for the first candidate and Bob for the second, thus their ballots will be ba = (enc(1), enc(0), enc(0)) and bb = (enc(0), enc(1), enc(0)). Thanks to the homomorphic property, the resulting tally will yield (enc(1)*enc(0), enc(0)*enc(1), enc(0)*enc(0)) = (enc(1), enc(1), enc(0)), which corresponds to the expected result when decrypted: (1, 1, 0)
The homomorphic encryption scheme used in Helios is called ElGamal.
ElGamal
The security of ElGamal is based on the hardness of solving a discrete logarithm, which is the operation of finding x given h, g and p such that h = gx mod p. In other words, it is easy to calculate h = gx but much harder to recover x = logp(h) in modular arithmetic. Let us see how this can be used to form an encryption scheme.
- Setup
-
Let the secret key
xbe a random number and let the public key beh = gx mod p.pis a large prime number publicly known, and all the following operations are calculated modulop.gis a generator of the cyclic group of orderp. - Encryption
-
Let the ephemeral key
rbe a random number, and calculate the shared secrets = hr. The ciphertext is the pair(gr, m*s). - Decryption
-
The shared secret can be recovered from the first part of the ciphertext and the secret key:
s = (gr)x = (gx)r = hr. Since the inverse of an element of the cyclic group can be calculated efficiently we can recover the original message in the following way:(m*s) * s-1 = m * (s*s-1) = m.
As mentioned before, two ciphertexts can be combined homomorphically to form an encryption of the product of the two messages. Indeed, the element-wise multiplication of the ciphertexts (gr1, m1*hr1) and (gr2, m2*hr2) yields (gr1+r2, (m1*m2*hr1+r2), which is the encryption of m1 * m2 with the ephemeral key r1 + r2.
Example
In the following example we examine the encryption, combination and decryption of Alice’s and Bob’s votes using ElGamal encryption. This illustrates how the ballots are encrypted in practice and should give a more concrete intuition of how the votes stay private. Additionally, this code snippet allows you interactively run the computation of the example.
Details of Alice’s and Bob’s encrypted ballots
-
Alice wants to vote for the first candidate and Bob for the second:
va = (1, 0, 0)andvb = (0, 1, 0) -
let
q = 53,p = 2q + 1 = 107andg = 75:ggenerates a subgroup ofZ/pZ(set of integers modulop) of orderq -
(note that we have not mentioned
qearlier for simplicity, but it does not change the rest of this example) -
let the key pair be
x = 18andh = gx = 35 mod p -
the encrypted ballots can be calculated as follows:
-
choose a random value, say
r = 2 -
encryption of the first element of Alice’s vote:
ba1 = (gr, hr * gm) = (61, 48 * 75) = (61, 69) -
note that the vote element
m = 1is projected ontoZ/pZbefore being encrypted, i.e. it becomesgm = g = 75 -
similarly for the first element of Bob’s vote with
r = 3:bb1 = (81, 75 * 1) = (81, 75)
-
-
the encrypted sum for the first candidate is:
c1 = ba1 * bb1 = (61 * 81, 69 * 75) = (19, 39) -
and once decrypted:
s1 = 39 * (19x)-1 = 39 * 69-1 = 39 * 76 = 75 = g1 -
the sum of the votes for the first candidate is indeed
1
Zero-knowledge proofs
Now that we know how the votes are kept private, the verifiability chain remains to be completed with proofs of proper encryption and decryption.
In general, a zero-knowledge proof is a protocol where a prover P attempts to convince a verifier V that she holds a piece of information without revealing anything about it. A typical example is Schorr’s protocol, where P proves to V that she knows the discrete logarithm x such that h = gx (in modular arithmetic).
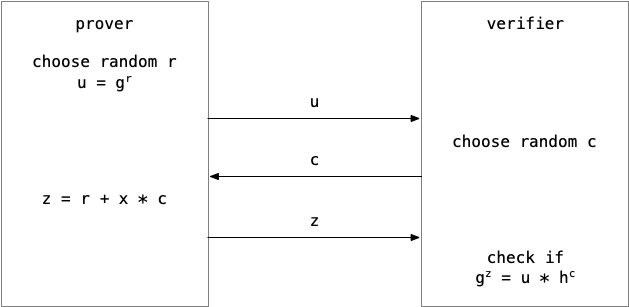
P first choose a random value r and commits to it by sending u = gr. Next, V choose a random challenge c and sends it back. Lastly, P sends z such that gz = u * hc and the only value satisfying this equality is z = r + x * c. P can only calculate z knowing x, thus V deduces that with a very high probability P indeed knows x such that h = gx.
It is possible to prove that the verifier, if she behaves honestly, does not gain any knowledge in the process. See this blog post for more insights.
A proof of this kind can be made non-interactive by using a so called Fiat-Shamir transformation, which replaces the challenge sent by V with the hash of a public value. A hash function is very hard to inverse, which means that a challenge chosen by hashing some value is hard to pre-calculate and can be considered random. In the case of Schorr’s protocol, P can hash g, h and u to form the following non-interactive protocol.
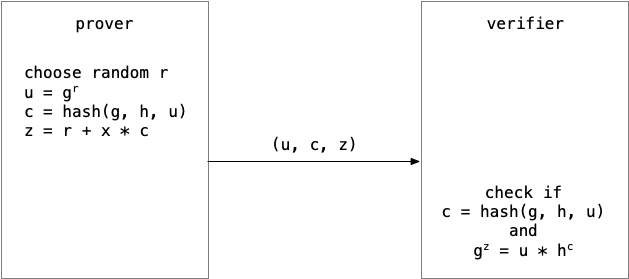
Application in Helios
In Helios, a zero-knowledge proof is used by each voter to convince an observer that its ballot contains only encryptions of 0 or 1. The statement that has to be proven is that either logg(gr) = logh(hr*gm) or logg(gr) = logh(hr*gm)/gm holds, respectively that either m = 0 or m = 1.
This is achieved with a disjunctive proof of log equality, see [Cortier2013] for a proper explanation.
Another zero-knowledge proof attests that the voting result is decrypted correctly. ElGamal encryption is basically an exponentiation of the plaintext, thus the decryption is similar to a discrete logarithm and its proof is based on Shorr’s protocol.
Attack on ballot privacy
As explained in [Bernhard2012], ElGamal as well as the Fiat-Shamir transformation used in Helios are malleable, which means that a ballot can be duplicated by re-randomization. An attacker can thus create a valid ballot containing the same vote as an existing one found on the public bulletin board.
For example, given the first part of Alice’s ballot ba1 = (gr, hr * g1) = (61, 69), anyone knowing the public key can generate a new valid ciphertext by adding a factor to the ephemeral key. Let u = 2, then ba1' = (61 * gu, 69 * hu) = (83, 102). This new ballot is equivalent to (gr+u, hr+u * g1) and is thus a valid encryption of 1 with randomness r' = r + u.
A possible consequence is that some malicious voters can collude against another one by duplicating its vote, which allows them to gain some information about it if they are numerous enough. In the extreme case, half of the voters could be malicious and the vote of their target could be determined with certainty by looking at the result of the voting process. Although the gravity of the breach might seem low since a high proportion of the voters have to be corrupted to lead to an actual leak, it shows that ballot privacy does not hold in certain cases and confirms the need for proofs of privacy under well defined conditions.
Implementation
This repo contains a simplified implementation of Helios without any dependencies: the necessary discrete algebra objects and cryptographic primitives are implemented from scratch. Additionally, the code aims to be as clear and simple as possible in order to show how the different parts of the scheme are put together. The strong typing of Scala helps to give expressive signatures to each function and make their role explicit.
Structure
We will go over the different layers composing the code in a bottom-up approach, going from the basic building blocks up to the final voting scheme.
The lowest layer of this implementation is the algebra package. It contains the logic about cyclic groups and finite fields on which the encryption is based.
trait Domain[Z: Integral, F <: Field[Z], G <: Group[Z, F], Gen <: Generator[Z, F, G]]:
val base: G
val exponent: F
val generator: GenThe Domain trait englobes a discrete group base, which is used later as the ElGamal public key space, with a finite field exponent, corresponding to the private key space. The generator projects elements of the exponent field on a subgroup of the base group. Note that Domain is "data type agnostic": the type parameter Z can be any type representing an integer - such as Int, Long or BigInt - in order to handle different sizes of numbers.
On top of this is built the crypto package. It contains an implementation of the ElGamal encryption scheme and the proofs of knowledge needed for Helios.
trait EncryptionScheme[PT, CT, PK, SK, D, R]:
val gen: (D, () => R) => (PK, SK)
val enc: (PT, PK, () => R) => CT
val dec: (CT, SK) => PT
trait HomomorphicEncryption[CT]:
val combine: (CT, CT) => CT
class ElGamal extends EncryptionScheme[...] with HomomorphicEncryption[...]:
...The EncryptionScheme trait is an example of the conciseness achievable in Scala: it states that the enc function takes a plaintext PT, the public key PK, a source of randomness R and returns a ciphertext CT. The other type parameters correspond to the secret key SK and the domain D.
As last layer, the voting package defines the VotingScheme trait and its main implementation Helios.
Helios
class Helios[N <: Nat]
extends VotingScheme[
SecretKey,
PublicKey,
Vote[N],
Ballot[N],
BulletinBoard[N],
TallyResult[N],
VotingResult[N],
DomainInt,
Random[Int]
]:
...
trait VotingScheme[X, Y, V, B, BB, TR, VR, D, R]:
val setup: (D, R) => (X, Y, BB)
val vote: (V, Y, R) => B
val cast: (B, Y, BB) => Either[BallotProcessingError, BB]
val tally: (BB, Y) => TR
val reveal: (BB, TR, X, R) => VRThe VotingScheme trait defines the five functions that a scheme has to implement to run a voting process. setup takes the domain containing the algebraic objects and a source of randomness to provide a pair of secret/public keys as well as a bulletin board. The vote function allows each voter to encrypt her vote and form a ballot, which they add on the bulletin board with the cast function. Note here that all objects are immutable, thus cast returns a new instance of bulletin board which should contain the added ballot. The tally function combines the ballots on the bulletin board into an intermediary result, which the reveal function decrypts using the secret key. A source of randomness is also needed for reveal to generate a randomized proof of decryption.
Helios takes a type parameter N representing the number of candidates in an election and defines concrete types for each of the type parameters of VotingScheme. The implementation of each function contains the wiring between the encryption scheme and the proofs on knowledge following the description in the previous section.
In order to illustrate how this implementation of Helios can be used, Main runs a demo with 3 candidates, 10 voters and one malicious voter. It also displays the content of each data structure to allow inspection from the vote until the result.
Result of sbt run
-------------------------------------------------- Random votes 0: 0 0 1 1: 0 1 0 2: 1 0 0 3: 0 1 0 4: 1 0 0 5: 0 1 0 6: 0 0 1 7: 0 0 1 8: 0 0 1 9: 0 1 0 Sum : 2 4 4 -------------------------------------------------- Setup Domain : p=107 q=53 g=75 Secret key: x=18 Public key: y=35 Proof of key generation: (10, 45, 14) Verification : true -------------------------------------------------- Encrypted ballots 0: ( 56, 49) ( 76, 23) ( 11, 34) 1: ( 69, 14) ( 75, 57) ( 99,105) 2: ( 86, 19) ( 75, 35) ( 23, 99) 3: ( 86, 83) ( 16, 44) ( 76, 23) 4: ( 19, 39) ( 33, 47) ( 1, 1) 5: ( 79, 81) ( 42,100) ( 4, 36) 6: ( 42, 37) ( 19, 69) (101, 92) 7: ( 44, 42) ( 75, 35) ( 81, 61) 8: ( 3, 25) ( 44, 42) ( 42,100) 9: ( 48, 86) ( 39, 49) ( 25, 87) 10: ( 99,105) ( 47, 76) ( 85,100) Proofs of ballot encryption 0: ( 9, 90,25,46) ( 56, 33,33,16) ( 69, 14,23,34) ( 56, 52,39,29) ( 99,105, 0,43) ( 37, 10,44,21) | ( 64, 16,42,36) ( 11, 19,31,21) | verification: true 1: ( 92, 33, 7,28) ( 81, 89, 6,13) ( 81, 85, 7,10) ( 57, 13,17,36) ( 35, 34,11,14) ( 39, 52,40, 9) | ( 4, 87, 8,23) ( 48, 86,51,33) | verification: true 2: ( 13, 79,52,12) ( 53, 89, 6,40) ( 25, 87,28,15) (100, 1,36,34) ( 30, 16,20,49) ( 39, 52,40, 4) | (101, 85,39,19) ( 1, 1, 2,19) | verification: true 3: ( 10, 52,33,24) ( 90, 52,26,21) ( 61, 64, 3,15) ( 23, 99,25,43) ( 27, 3,49,31) ( 14, 52,25, 6) | ( 39, 35,30, 1) ( 16, 12,31,35) | verification: true 4: ( 16, 10,26,46) ( 35, 34,32,19) ( 10, 52,41,22) (101, 30,33,49) ( 16, 12,52,22) ( 36, 14,17,39) | ( 64, 48,28,31) ( 33, 47,32, 4) | verification: true 5: ( 13, 41,45, 5) ( 87, 39,10,15) ( 33, 49,49,12) ( 35, 34,10,34) ( 56, 49, 3,21) ( 92, 89,31, 4) | ( 30, 40,12,39) ( 53, 89,38,15) | verification: true 6: ( 69, 14,42,30) ( 30, 30,44,41) ( 56, 49,21,40) ( 12, 49,23,34) ( 41, 35,20,27) ( 92, 33,34, 8) | ( 40, 27,32,29) ( 14, 40, 2, 8) | verification: true 7: ( 83, 57,14,50) ( 49, 75,20,39) ( 61, 48,35,37) ( 57, 90, 3,22) ( 11, 92,24,34) ( 35, 34,37,23) | ( 79, 90,29,31) ( 23, 99, 6,44) | verification: true 8: ( 81, 75,42, 8) ( 13, 44,18,11) ( 64, 4,41,39) ( 13, 1,45,28) ( 13, 13,37, 9) ( 90, 79,52,36) | ( 4, 87, 8,47) ( 53, 89,40,42) | verification: true 9: ( 49, 92,48,28) ( 76, 83,34,21) (105, 19,41, 0) ( 10, 52,18,47) ( 1, 1, 2,27) (105, 13,31, 0) | ( 12, 30,13,23) (101, 64,47,51) | verification: true 10: ( 49, 92,48,46) ( 76, 83,34,47) (105, 19,41,22) ( 10, 52,18,14) ( 1, 1, 2,41) (105, 13,31, 5) | ( 12, 30,13,31) (101, 64,47,31) | verification: true -------------------------------------------------- Tally result ( 3, 27) ( 76, 9) ( 23, 85) -------------------------------------------------- Voting result Sum : 2 5 4 Proof of decryption: ( 34,39,21) ( 86, 3,15) ( 87, 5,13) Verification : true --------------------------------------------------
Conclusion
Diving into the subject of voting schemes allowed us to discover some desirable privacy and verifiability properties in voting schemes and to see how they can be provided by leveraging existing cryptographic constructions. We introduced the concepts of homomorphic encryption and zero-knowledge proof, and we went over a simplified implementation of the Helios 2.0 voting scheme.
We also described an attack on ballot privacy, which gives a concrete example of the need for continuous research in the field of voting systems. Democratic decisions are at the core of our society and the population needs to trust the process of taking them.
References
-
[Adida2009] B Adida, O De Marneffe, O Pereira, J Quisquater. Electing a university president using open-audit voting: Analysis of real-world use of Helios. EVT/WOTE. 2009.
-
[Bernhard2011] D Bernhard, V Cortier, O Pereira, B Smyth, B Warinschi. Adapting Helios for provable ballot privacy. European Symposium on Research in Computer Security. 2011.
-
[Bernhard2012] D Bernhard, O Pereira, B Warinschi. How not to prove yourself: Pitfalls of the fiat-shamir heuristic and applications to helios. International Conference on the Theory and Application of Cryptology and Information Security. 2012.
-
[Cortier2013] V Cortier, B Smyth. Attacking and fixing Helios: An analysis of ballot secrecy. Journal of Computer Security. 2013.
